AB = CF = 8 COUDÉES
BC = 5 COUDÉES
d'où, AF= 8+5+8 = 21
et AC = 8+5=13 COUDÉES
AF/AC = 21/13 = 1,6154 le rapport 55/34 = 1,6176

---

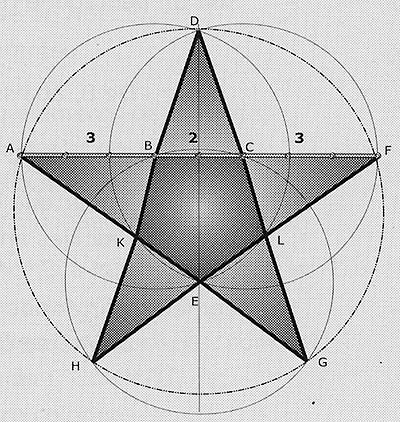
A l'aide d'une corde à noeuds, tracer un segment de droite de 21 coudées (AF)
en marquant, par rapport à A, les points 8 coudées par B et 13 coudées par C.
Tracer un cercle de centre B de rayon BA= 8 coudées
puis un cercle de centre C de rayon CF égal aussi à 8
Ces deux cercles se coupent en D et E
Les droites AE et DC se coupent en G et les droites DB et FE se coupent en H,

le pentagramme est tracé.

---

Nota: ce tracé détermine aussi deux pentagones inversés:
le pentagone BCLEK et, celui obtenu en joignant ADFGH
Si le pentagramme ADFGH, est dterminé par un rapport approché (8/5 = 1,6 ) le tracé est visuellement incorrect
les points DBKH ne peuvent être alignés pour respecter les intersections entre les cercles utilisés pour le tracé
et le cercle circonscrit au pentagramme (tracé ci-contre)